「42を3つの立法数の和で表わせ」長年未解決だった数学の難問が解明される

「僕にはもう時間がない」　19歳で決闘で死んだ天才数学者ガロア

数学の世界には、一般の人々には到底理解できない難問が多数存在しています。

その1つが、今回話題になっている「1から100までの自然数を3つの立方数の和で表現する」という問題です。

「なんでわざわざ解くの？」のという問題はとりあえず置いておくとして、この問題には実に64年間も未解決となっている解が存在します。

それが「33」と「42」になる場合の3つの立方数の組み合わせです。

英国ブリストル大学のAndrew Booker氏は、33の解については2019年3月に報告していますが、それからほんの半年ほどの時間で、続けて42の解も発見したのです。

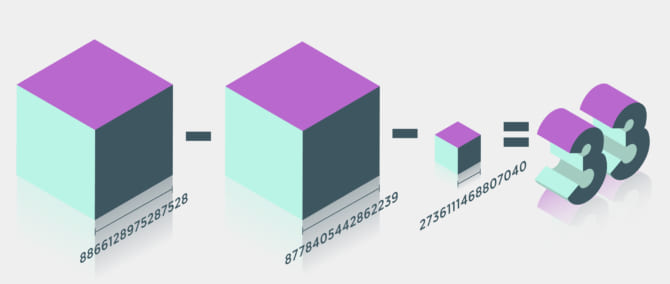
ちなみに答えが33となる3つの立方数の組み合わせの解は、

33 = (8866兆1289億7528万7528)³+(-8778兆4054億4286万2239)³+(-2736兆1114億6880万7040)³

となるそうです。42の場合はこれよりさらに巨大な数字になりました。この数字を見ると、今まで発見できなかったのも無理はないと理解できるでしょう。

この飛んでもない「42の解」発見のニュースについては、9月6日付けでブリストル大学よりプレスリリースが発表されています。

3つのキューブで自然数を表現する

聞いただけでは意味が取りづらいこの問題は、もともとは1954年にケンブリッジ大学より提示されました。

問題の内容を簡潔に記述すると「n = a³+ b³+ c³ (nは1から100までの自然数）を満たす整数abcの組み合わせはなんでしょう？」となります。

基本的に数字の3乗というのは、立方体の体積を表す数となるので、これを立方数とかキューブと呼びます。

この問題を解くことに何の意味があるのか、というのは数学者でないと理解しづらいものですが、これはディオファントス問題と呼ばれるものの1つで、ある方程式の整数解を求める数論では非常に重要なテーマの1つです。

ディオファントス方程式はたいていは解があるかどうかを事前に判断する方法がありません。そのため、方程式を満たす解が存在するかどうか調べること自体が研究テーマになるのです。

有名な『フェルマーの最終定理』もこのディオファントス方程式の仲間になります。（フェルマーの最終定理について知りたい人は、こちらの記事を参照してください）

この問題は2000年に、ほとんどの解が発見されました。しかし、nが33と42の場合だけは、2019年になった時点でも解が見つかっていなかったのです。

(ちなみに、この問題で数字を9で割ったとき余りが4または5になる数には解が存在しません)