歴史で学ぶ量子力学【2】※本記事
歴史で学ぶ量子力学【3】
20世紀のはじめ、第一次大戦が終りを迎えた頃、物理学は光の「波動説」と「粒子説」の2つの間で揺れていました。
光が矛盾するどちらの性質でも成り立ってしまうことに皆が困惑していたのです。
1922年にアーサー・コンプトンによるコンプトン効果の発見によって、アインシュタインの光量子仮説は決定的なものになっていました。
コンプトン効果とは、電子にX線をぶつけたとき、弾かれて散乱したX線の波長が伸びるという現象です。波長が伸びるということは、X線がエネルギーを失っていることを意味しています。
衝突でエネルギーを失うという現象を古典物理学で説明するなら、ビリヤードのようにぶつかった玉が運動量の一部を相手に奪われた、ということになります。
波は運動量を持たないため、古典物理学の解釈ではX線を波と捉えたまま、散乱で波長を伸ばす理由が説明できませんでした。当時の物理学がコンプトン効果を理解するためには、X線が粒子であると解釈しなければならなかったのです。
こうして、この時代の物理学者たちは、月曜と水曜と金曜は光の波動論を教え、火曜と木曜と土曜は光の粒子論を教えなければならない、と冗談交じりに愚痴るような状況になりました。
では、ここから物理学は一体どこへ向かっていったのでしょうか?
物質の全ては波
粒子と波動、どちらも成り立つこの問題に最初の光を当てたのが、物理学者としては異例の系譜を持つフランス公爵家出身の貴公子ルイ・ド・ブロイでした。

彼はX線を研究する兄モーリスの影響で物理学にはまっていき、兄が公爵家を継ぐために科学の道を諦めたため、その意志を引き継いで物理学者になりました。
ド・ブロイの発想は非常に画期的でした。彼は光が粒子なのか、波なのかという論争を物理学者たちが繰り広げる中で、次のようなことを考えたのです。
「波であるはずの光が粒子のように振る舞うのだとしたら、原子などの粒子は波のように振る舞うのではないだろうか?」
彼はこの考えに基づき、当時太陽の周りを回る惑星のように原子核の周りを軌道を描いて回る粒子だ、と考えられていた原子内の電子を、定在波であると仮定した論文を書いたのです。
彼のこの仮説には、ボーアの原子モデルにとっても重要な意味を持ちました。
新しい原子モデルを考え出した当初、ボーアは定常的な軌道を回る電子はエネルギー放射を行わないため、原子核に落ちることが無いと仮定しました。しかし、彼は「なぜ電子がエネルギー放射をしないのか?」という疑問に答えることはできなかったのです。
もしド・ブロイの主張する通り、電子が粒子でなく波なのだとしたら、それは加速することがありません。加速しなければ電子はエネルギー放射をすることもなく、したがって原子核に落下することもないのです。
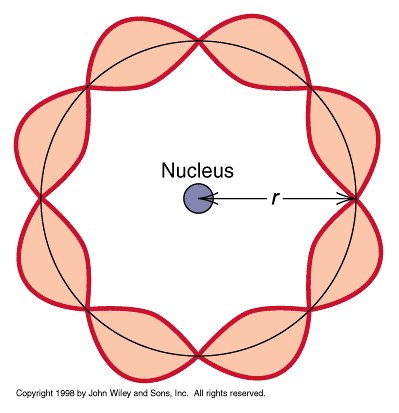
しかも、ド・ブロイの原子核を回る電子の定在波は、ぐるりと円を描いて繋がっているため波形の崩れる位置でつなげることができません。
軌道の長さは、必ず電子の波長の整数倍でなければならず、それはボーアの主張する電子の軌道とピタリと一致したのです。つまりボーアの主張する定常的な軌道がなぜ存在するかも、ド・ブロイは同時に説明できたのです。
しかし、あまりに突拍子の無いこのアイデアに、多くの物理学者は困惑してしました。なにせ、この論文はド・ブロイが学位取得のために書いた博士論文だったのです。
けれど、この論文を手放しで評価した人物が現れました。それが、光電効果によるノーベル賞受賞と、一般相対性理論の発表をほぼ同時期に果たして、一躍時の人となっていたアインシュタインでした。
当時の物理学会にとってアインシュタインの太鼓判は、ド・ブロイの考えを受け入れるのに十分な理由でした。
しかし、「粒子だと思っていた電子が波である」などという主張はどうやって証明すればいいのでしょう?
ド・ブロイはそれについて、電子が波の性質を持つならば、電子も回析を起こすはずだという予想を述べました。このド・ブロイの予想は、後に複数の物理学者たちの実験によって証明されます。
その中の一人が、ジョージ・トムソンでした。この功績によりジョージ・トムソンはノーベル物理学賞を受賞します。ちなみに、彼の父、J・J・トムソンは電子が粒子であることを発見し、ノーベル物理学賞を受賞した科学者です。
トムソン親子は驚いたことに、それぞれ「電子は粒子である」「電子は波である」と証明して、親子二代でノーベル賞を受賞したのです。
「あーもうめちゃくちゃだよ!」と思った物理学者もいたことでしょう。
ともあれ、こうして、光も電子も「波でありながら粒子の性質を示す」という二重性の考え方が物理学の世界に受け入れられることになったのです。