- ABC予想が8年の査読を経てようやく論文誌掲載へ
- ABC予想の証明は既存の定理を証明するだけでなく未知の定理や法則も内包している
- 証明に使われた「宇宙際タイヒミュラー理論」では数学の常識が破壊されていた
- ABC予想の証明にはSF的な未来を構築する理論が含まれているかもしれない
京都大学の望月新一氏によって、数学界で最大の問題であると言われる「ABC予想」が解明されました。
実は証明自体は2012年に「nature」に提出されていたのですが、理論があまりにも難解で、検証に8年もかかっていたとのこと。
「ABC予想」のスゴいところは、証明することができれば、既知のあらゆる数学理論を説明するだけでなく、まだ発見されていない数学理論の証明にもつながるという点です。
フェルマーの最終定理の証明は、フェルマーの最終定理しか証明しませんでしたが、「ABC予想」が証明された場合、フェルマーの最終定理はただちに証明されるほか、
既存のあらゆる数学的な問題に対して、等しく証明を与えることになります。
それどころか「ABC予想」は、まだ存在が知られていない無数の定理に対しての証明にもなっていることが予想されるのです。
アインシュタイン一般相対性理論があらゆる物理理論の基礎になっているように、「ABC予想」は無数の公式の母となる力をもっているのです。
では次は、ABC予想が一体どんなものかを説明したいと思います。
カンタン?なABC予想解説!
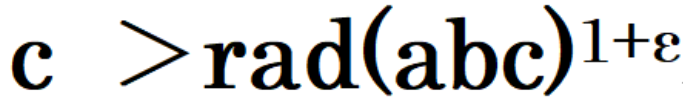
ABC予想とは、3つの自然数の特別な関係を証明したものになります。
予想がどのようなものであるかを理解するには「rad」という、簡単な概念を理解するだけで十分です。「rad(●)」とは、「●の部分にある数字の中にある素数だけを掛け合わせて下さい」という記号で、「根基 (radical) 」の略です。
大丈夫です。すごーく簡単で、簡単すぎることをなんでこんなに難しく書くんだ? と問いたくなるレベルですから。
ではまずは、「rad(8)」を例にとります。
8は2の3乗なのでrad(8)はrad(23)と書き直すことができます。
ここまでは、大丈夫ですよね?
流石に8=23がわからない人は…いません、よね?
このときrad(23)の答えは、乗数を無視して「2」になるんです。
rad(23)=「2」
え、それだけ?
と思うかもしれませんが、「rad」はそれだけの簡単な概念なのです。
同じように、
rad(25)はrad(52)となり、答えは乗数を無視した「5」になります。
またrad(50)など乗数だけでは表せないものについては、掛け算の組み合わせに分解します。
つまり…
rad(50)=rad(25×2)=rad(52×2)となり、あとは乗数を無視して掛け算(5×2)を行い、rad(52×2)=5×2=10となります
またrad(45)のときは…
rad(45)=rad(9×5)=rad(32×5)=3×5=15
になります。
さて、radがわかったところで、いよいよABC予想の根幹を示します。ABC予想とは、3つのa,b,cという数が、任意(適当)の数「ε」のもとに、
という数を満たす「a,b,cの組み合わせが、ほんの数個しかないことを証明する問題」だったのです。
radの次のカッコの中に「abc」と固まっている部分は「a×b×c」という意味です。
一見すると、簡単に証明できそうですね。
でも、誰も証明できなかったんです。そう、望月教授を除いては。