迷路を数学的に解剖してみる
迷路の攻略を数学者の視点から考える場合、必要となる考えは「柔らかい粘土で作られた素材を切り貼りしないで変形させる」という概念です。
この概念は「位相幾何学(トポロジー)」として知られています。
なにやら難しそうな呼び名ですが、言いたいことは単純です。
トポロジーでは物体を自由に変形できる粘土のように捉えています。そのため物体の形を区別する要素は、その物体に穴が空いているか? その穴はいくつあるか? という要素だけになります。
たとえば、トポロジーでは取っ手が一つだけついたコーヒーカップと、ドーナツは同じ種類の形として扱われます。これはどちらも穴が一つです。
イマイチ納得行かないという人は、粘土のドーナツをぐにゃぐにゃと変形させて、取っ手が一つのコーヒーカップを作ることを想像してみましょう。
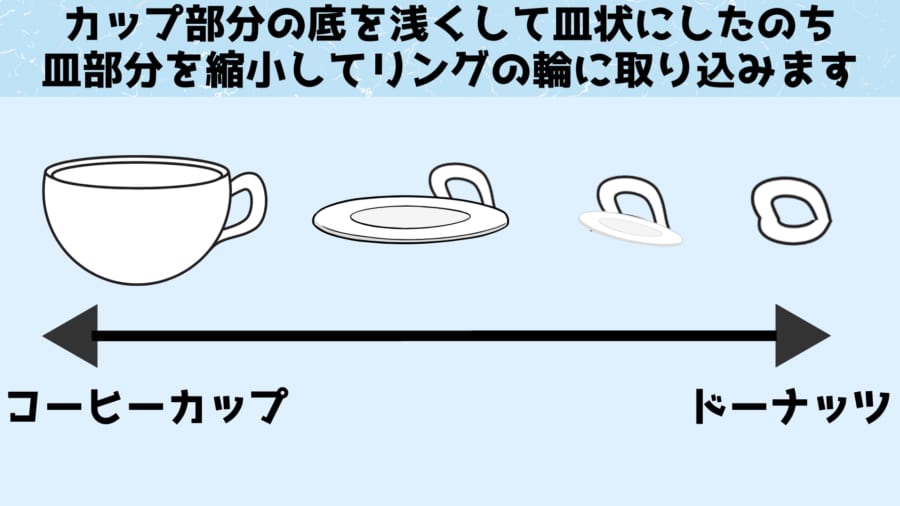
リングの一部分に粘土を集めつつカップを作れば、一度も粘土をちぎることなくドーナツからコーヒーカップを作れます。
逆に、上の図のように、コーヒーカップのカップ部分を平らにして、リング全体に均一になるよう捏ねていけばドーナツの形にすることができます。
このように伸び縮みする柔らかな素材を使うと、コーヒーカップとドーナツは1度もどこかを切り取ったり穴を開けたり、新たな接続部分を作らずに、滑らかに変形させていくだけで形状を行き来することが可能です。
この状態をトポロジー的には同じであると表現します。
このトポロジーの考え方を理解すると、「入口で片手を迷路の壁について歩き続ければいずれ出口にたどり着ける」という迷路攻略法がなぜ成立するのかという問題も解決できます。
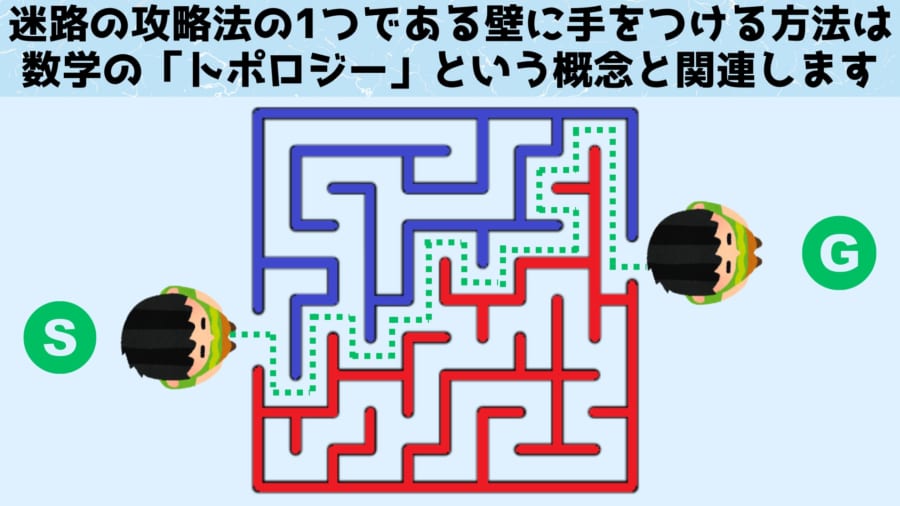
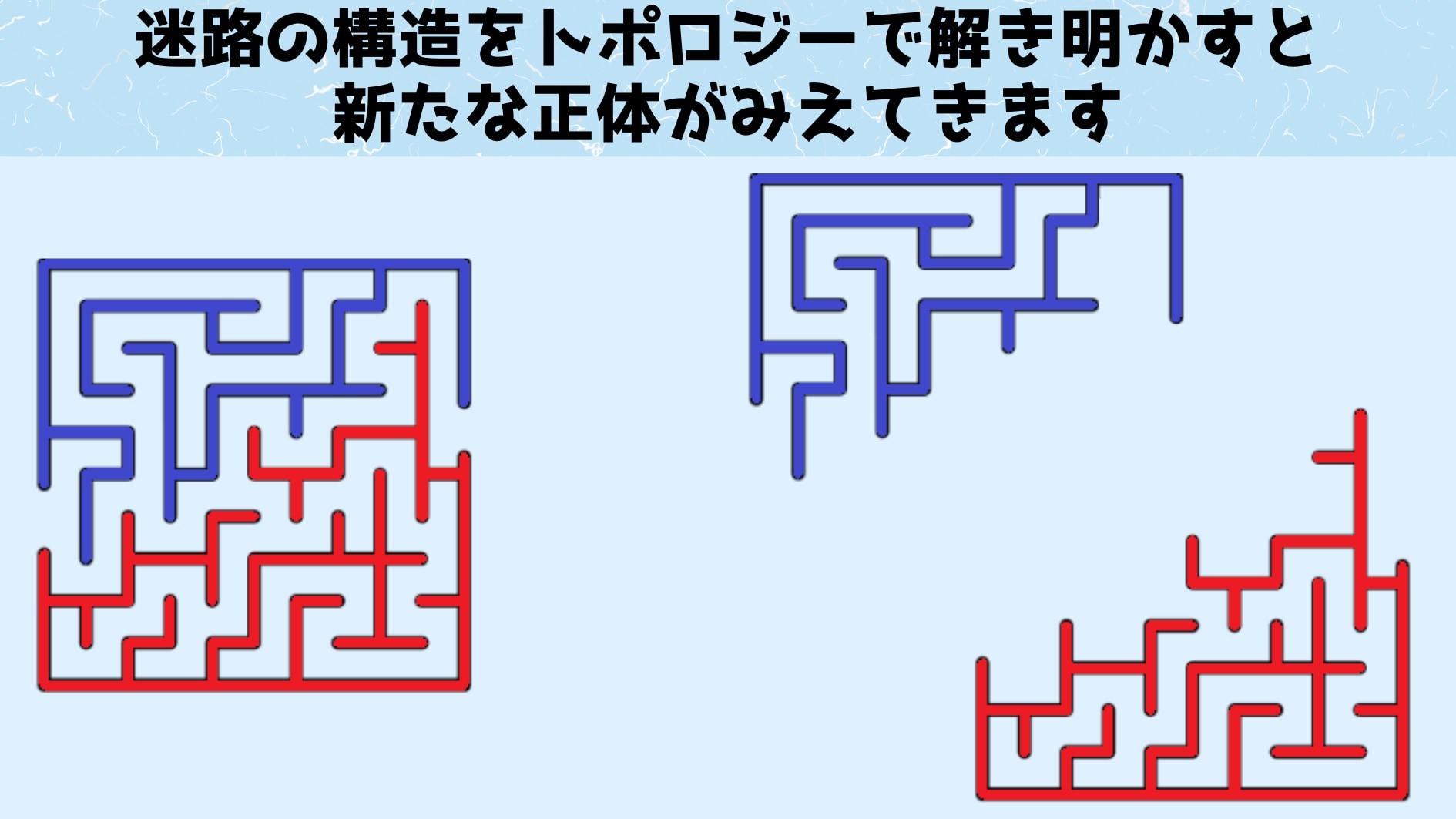
上の図は、スタートとゴールが端と端にある標準的な迷路を最短距離で攻略するルートを示しています。
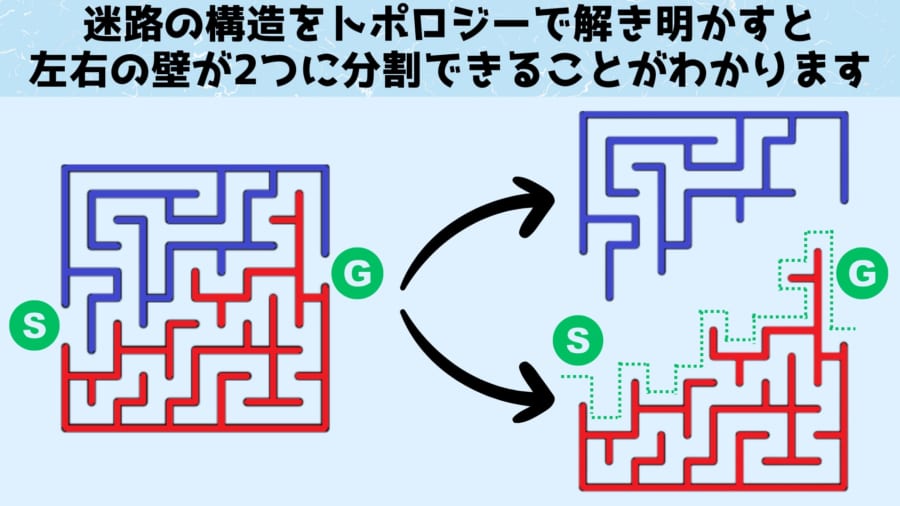
興味深いことに、迷路の左手側(青色)と右手側(赤色)を掴んで引っ張ると、この最短ルートは迷路を2分割する境目であることがわかります。
逆に言えば最短ルートとは、両側の壁の分割ラインだったと考えることもできます。
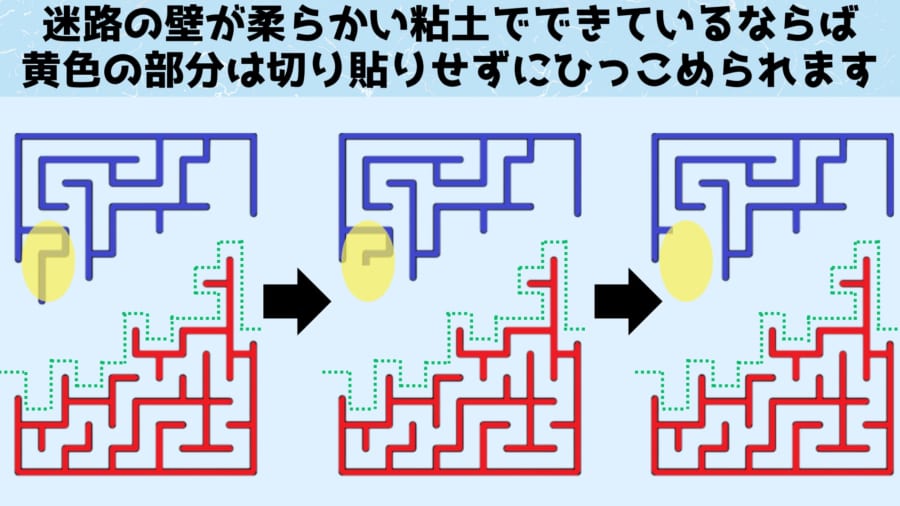
ここで先ほどのコーヒーカップとドーナッツの例のように、迷路の壁が柔らかい素材でできていると考えると、黄色で囲った「飛び出ている壁」を引っ込めても、トポロジー的には同じと言えます。
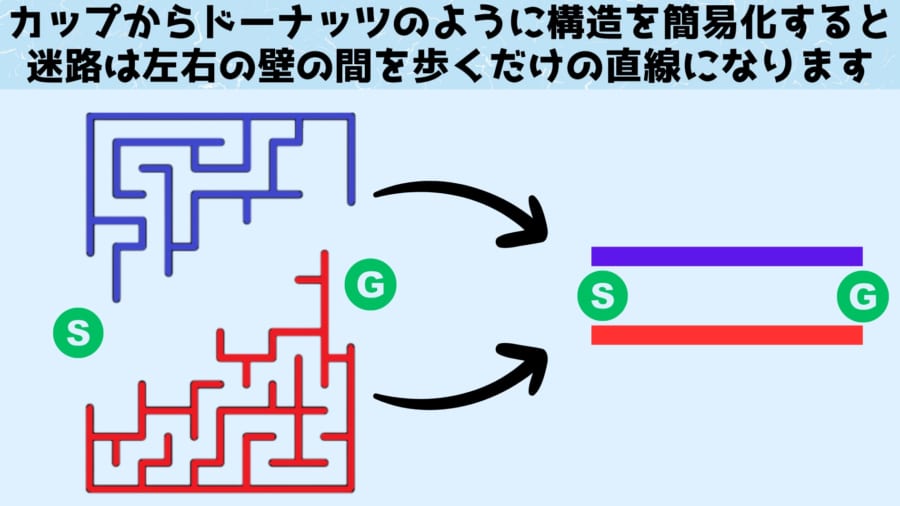
同様に飛び出ている壁を切り貼りせずにどんどんひっこめていくと、迷路は最終的に2つの壁に挟まれた直線ルートに変形させることができます。
この状態で「壁に手をあてる攻略法」を当てはめてみると、この攻略法とは、トポロジー的に同じという概念に基づいてゴールに向かっていることがわかります。
この考えは、より複雑な迷路でも機能します。
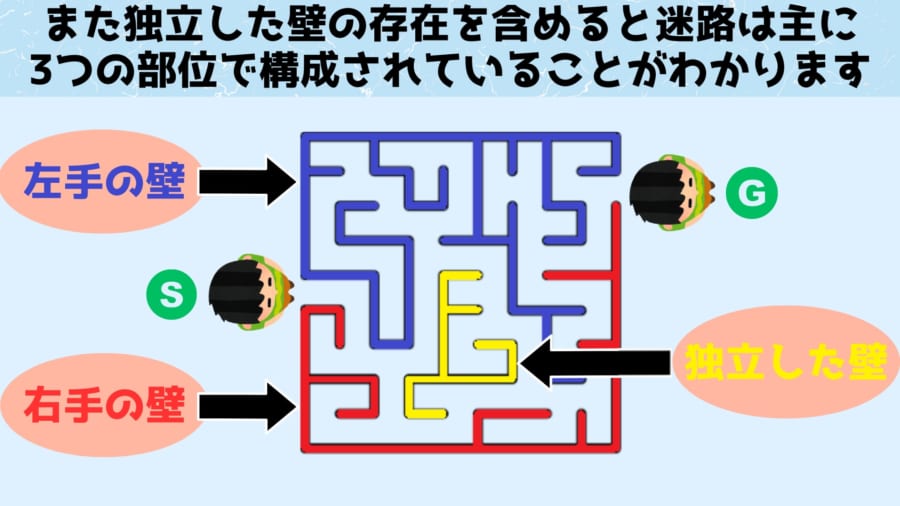
上の迷路は先ほどの迷路に黄色い「独立した壁」という概念を加えたものです。
この独立した壁は左手の壁と右手の壁のどちらとも接続していないことがわかります。
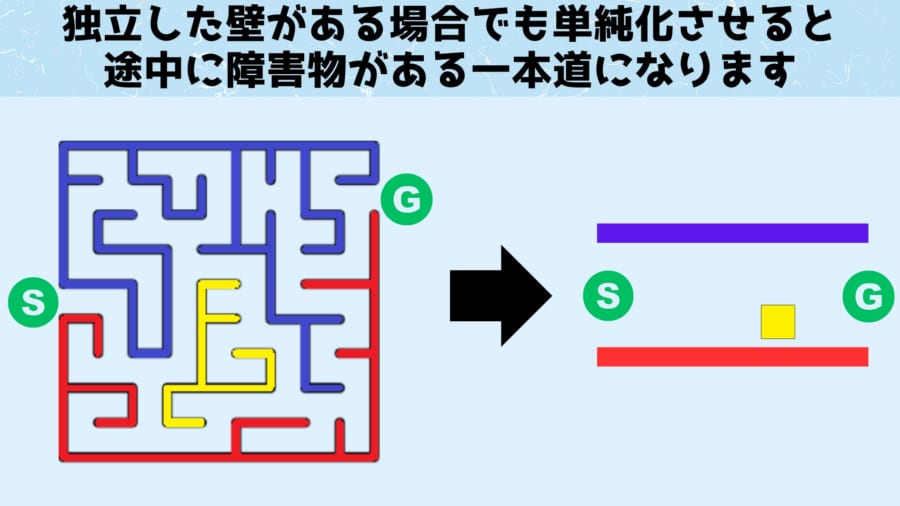
この迷路に対しても先ほどのように、分割して壁を引っ込めるトポロジー的に同じ処理を行うと、最終的には左右の壁とその間に挟まれた黄色い塊へと変形させることが可能です。
中央に独立した壁であっても「手を壁に当てながら進む」で攻略できるのは、このためです。
ではゴール地点が迷路の中心にあるような、特殊なパターンではどうなるでしょうか?
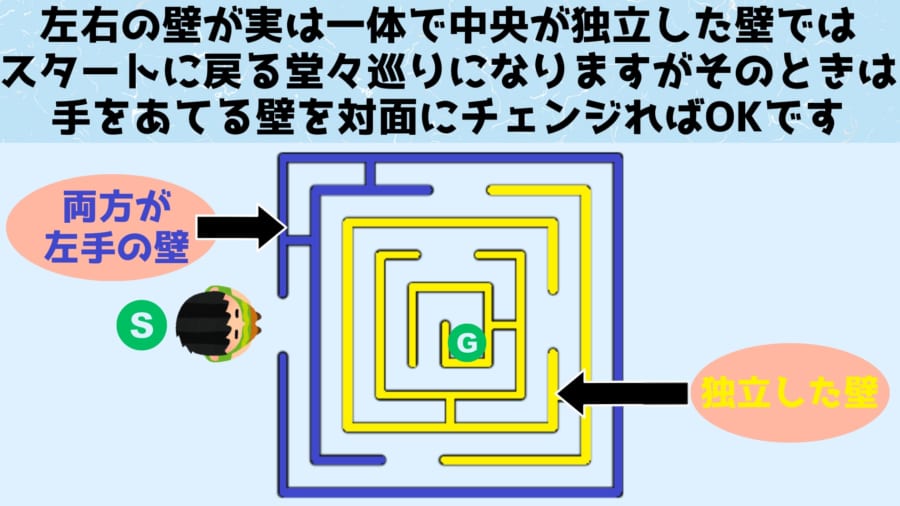
上の図はそのパターンを示しており、スタート地点の壁は分割できない「両方が左手の壁(あるいは右手の壁)」の状態になっており、その先には独立した壁に囲まれたゴールが存在しています。
この場合「手を壁に当てながら進む」を実行すると、必ずスタート地点に戻って来てしまう堂々巡りが起きてしまいます。
そこでこの迷路に対してもトポロジー的に同じになるように処理してみます。
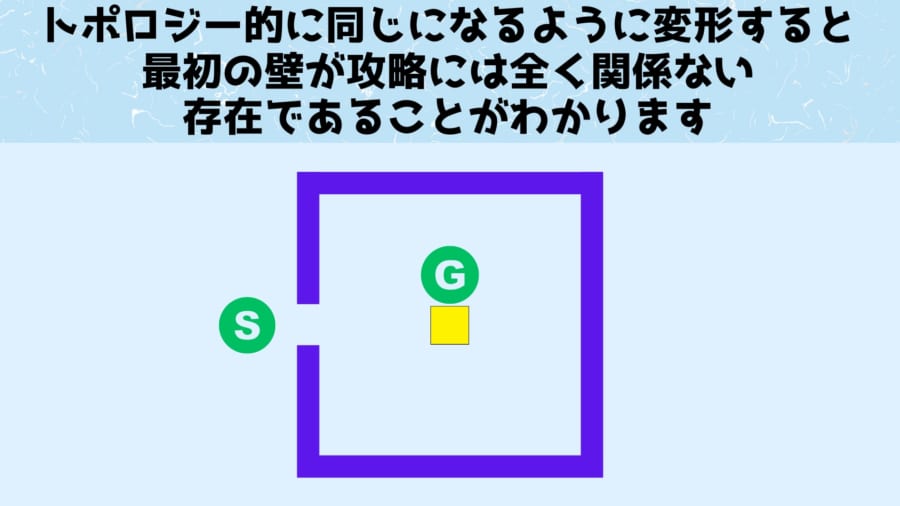
すると最初の「両方が左手の壁」はゴールに繋がっておらず、ある意味で攻略には全く関係がない存在であることがわかります。

これをトポロジー的に際立たせると、上の図のようになります。
この図を見ると、最初に接触する両方とも左手の壁(青)にどんなにアプローチしても黄色の壁に囲まれたゴールにたどり着けないことがわかります。
つまり「手を壁に当てながら進む」方法で堂々巡りになってしまう場合、手を当てている壁が攻略に関係ない存在と判断することが可能になります。
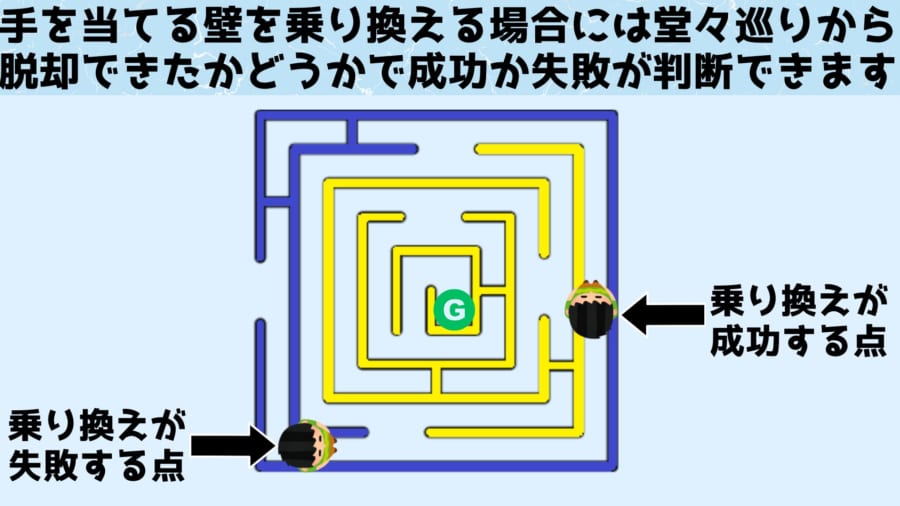
なのでその場合には、手をあてる壁を対面の壁に変換させ、堂々巡りから抜け出せたかを確認する作業が必要になります。
こうすることで、攻略に関係ない壁から攻略に関連した壁に移ることが可能になります。
ただその場合には、壁の乗り換えを行う地点が重要になります。
上の図のように、両方が左手の壁であると、乗り換えを行っても堂々巡りからは脱出できません。
そのため中央に独立した壁に囲まれたゴールがある迷路は、両端にスタートとゴールがある迷路に比べて必勝法の適応に試行錯誤が必要となるでしょう。
迷路は人間を迷わすことを目的として作られています。
しかし迷路を数学者の視点から(トポロジー的に)考えるとその本質は「必ず攻略できる一本道」であることが理解できたかと思います。
たとえどんなに独立した壁の存在が多くとも、迷路に組み込めるピースの数は有限です。
どんなに時間がかかっても必ず脱出できるでしょう。