メビウスの輪とは

メビウスの輪とは、長方形の紙を180度ひねって端と端をくっつけたものです。
紙の表をなぞっていくと裏につながったり、裏をなぞっていくと表になったりと、表と裏が同時に存在しているという不思議な特徴があります。
その特徴と形からして、無限(∞)を表すものとしてよく例えられます。
2024.06.20 Thursday
2018.04.24 Tuesday
小さい頃、ちょっと変わった紙細工で遊んだことはないでしょうか?
表と裏がくっついている不思議な図形。そう、メビウスの輪です。
目次

メビウスの輪とは、長方形の紙を180度ひねって端と端をくっつけたものです。
紙の表をなぞっていくと裏につながったり、裏をなぞっていくと表になったりと、表と裏が同時に存在しているという不思議な特徴があります。
その特徴と形からして、無限(∞)を表すものとしてよく例えられます。
カテゴリー覧
人気記事ランキング
Amazonお買い得品ランキング
数学のニュースmathematics news
もっと見る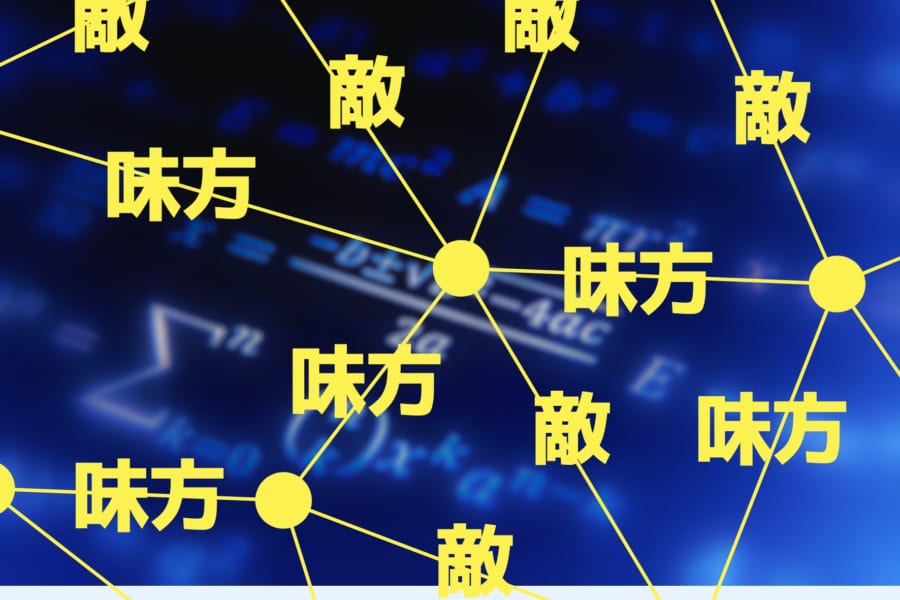
「敵の敵は味方」であることを数学が証明!人間関係の新理論

長方形と帯はどこが境目?「メビウスの輪が作れる」アスペクト比の研究
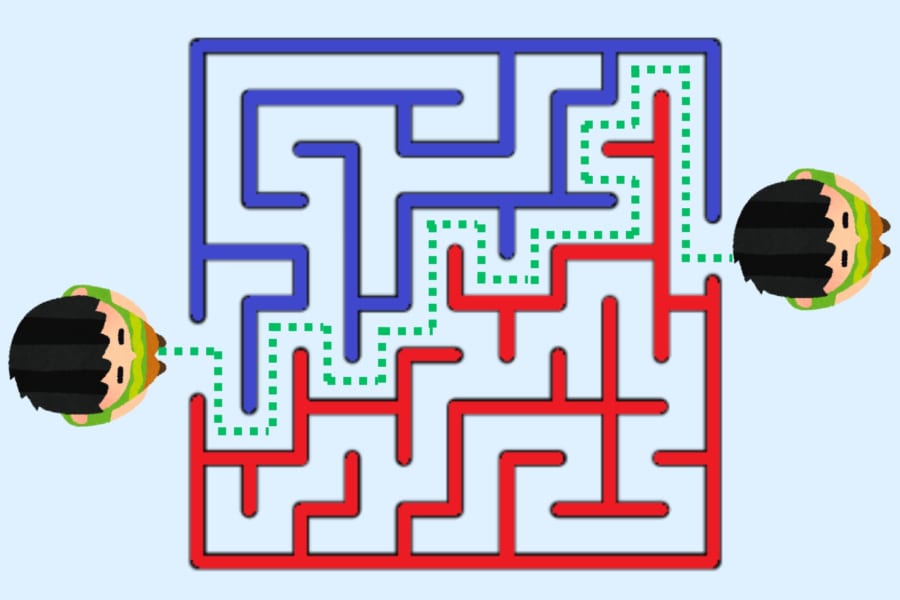
数学の概念を使ってなぜ迷路は「手を壁に当てる」と攻略できるのかを解説
注目の科学ニュースpick up !!

【ガチ不老】信長より前から生きてるニシオンデンザメ(512歳)は老化していなかった
致死率ほぼ100%、皮膚から湧き出す「最凶の寄生虫」の全ゲノムを解読

「何しても楽しくない」退屈な日々を一気に楽しくする”簡単な方法”