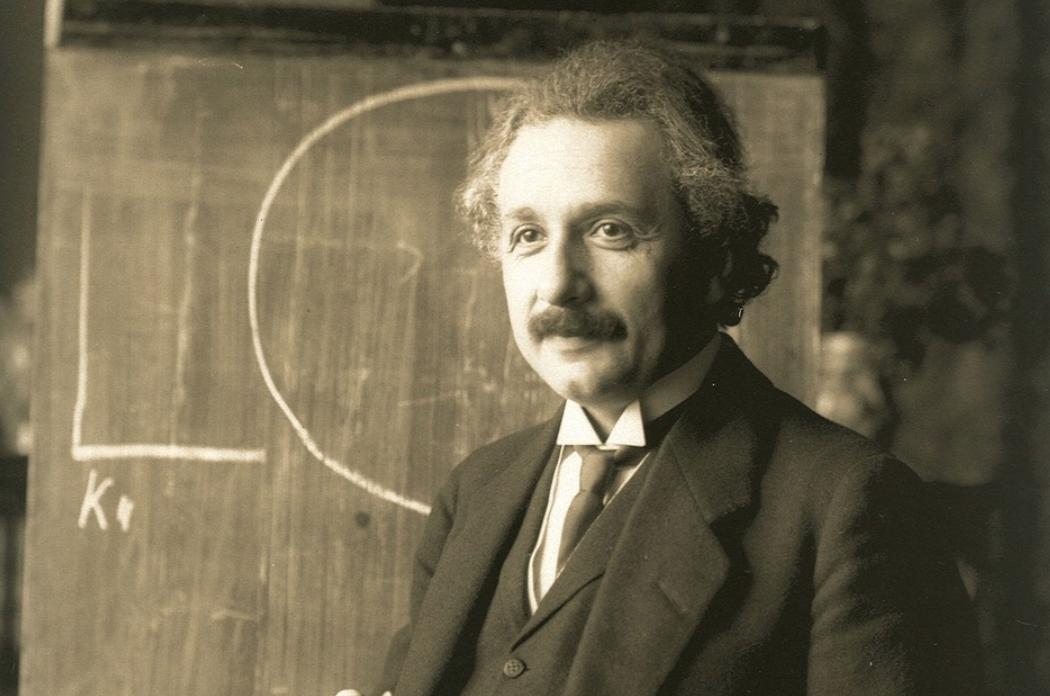
歴史で学ぶ量子力学【2】
歴史で学ぶ量子力学【3】(近日公開)
「観測するまで物事の状態は決定されない」「全ては確率」
そんな中二心をくすぐるワードでいっぱいの量子力学ですが、私たちに見える世界はそんな曖昧なものではなく、もっと盤石で決定論的なものに見えます。
アルベルト・アインシュタイン博士は量子力学を生み出した功労者の1人ですが、最後までこの曖昧な量子力学の考え方を受け入れることはできませんでした。
量子力学の発展に大きな貢献をしたエルヴィン・シュレーディンガー博士も、同じく量子力学の主張する確率解釈を受け入れることはできませんでした。
シュレーディンガーに至っては「私の波動方程式がこんな風に使われるのなら、論文などにしなければよかった」と嘆いたほどです。
しかし、量子力学はその不可思議な主張を柱にしながら、大成功を収めた理論であり、現代ではほぼ完全に受け入れられてしまっています。
SFネタとしては興味深いですが、現実の話としてはずいぶんと突飛で難解な量子力学。
これらは一体どのようにして発見され、今に至ったのでしょうか?
ただ解説されるだけでは難しすぎる量子力学の世界を、ここでは歴史の観点から追ってみましょう。
量子の発見

量子力学の歴史はマックス・プランクの黒体放射の研究から始まります。これは光のエネルギーと色の関係を調べる研究でした。
ガスバーナーやコンロの炎は赤色より青色の方が温度が高く、夜空の星々も赤より青く輝く方が高温の星です。
熱した物体は光を放ちますが、これは温度によって色が変わります。これは古くから知られている事実でした。
しかし温度と色にどういう関係性が成り立つのか? という問題は長らく謎のままでした。
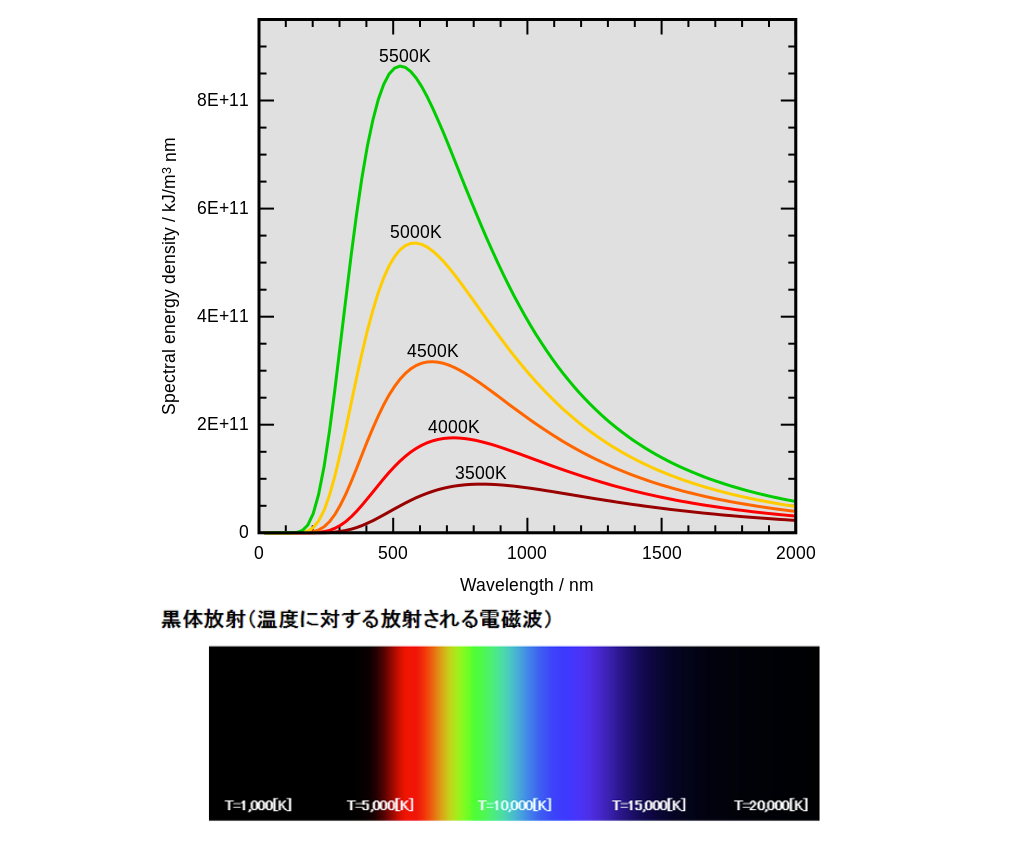
温度とはすなわち光の持つエネルギー量を意味しており、色は光の波長によって決まります。温度と色が相関関係を持つということは、光は波長(振動数)でエネルギー量が決まっているはずです。
しかし、こうした考えで作られた方程式は、なぜか長波長(赤外領域)に向かうほど実験結果と大きな誤差を生んでしまいました。
なぜ波長が伸びるほど、計算と実験結果はズレてしまうのでしょうか?
波長が短くなると、振動数は増えることになります。実験結果は振動数が大きいほどエネルギー量も大きくなることを示していました。
そこでプランクは、もっとも単純な解決策として、振動数に定数を掛けるというアイデアを採用します。
そして、光が1回振動するときに現れる最小エネルギー量を実験結果から導き出し、定数として方程式に組み込んだのです。
それが「E = hν」という数式です。Eとは光のエネルギー、ν(ギリシャ文字「ニュー」)は光の振動数を表します。そしてhが導入された定数が「プランク定数」です。
プランク定数hは6.626 × 10-34という恐ろしく小さい値で、日常的なスケールではまず気づくことのできないものです。
こうして作られたプランクの式は、ピタリと実験結果と一致しました。
しかし、プランクはこれを単に計算の辻褄を合わせるためにやった窮余の策と考えていました。
なぜなら、プランク定数の意味を考えた場合、それは光が連続した波ではなく、「hν」という飛び飛びの値で変化する粒子ということになってしまうからです。
プランクは光の正体が波ではなく、決まったエネルギー素量を持つ粒子であるとはとても考えられなかったのです。
しかし、この「hν」という塊は、後に量子と呼ばれることになり、物理学の様々な局面で重要な意味を持つようになるのです。